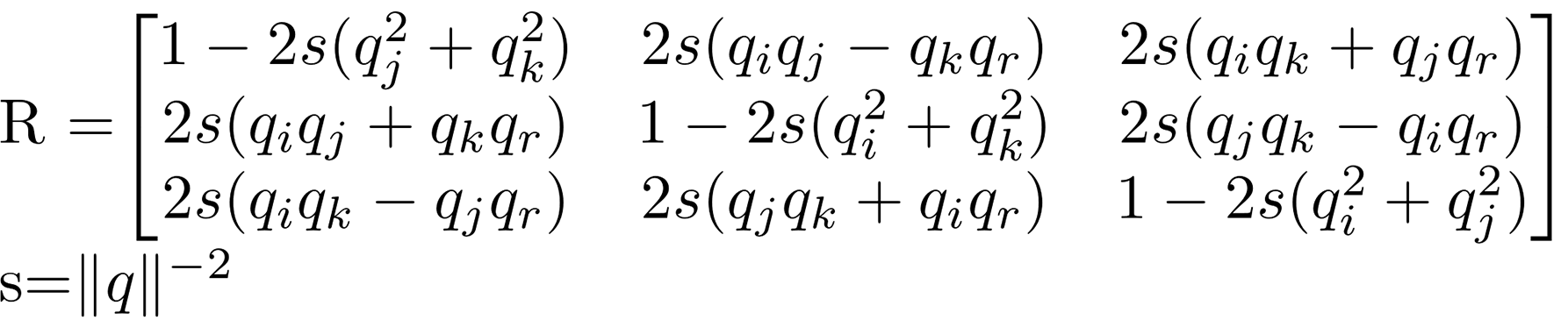Virtana Internship Week 1
I have started my internship at Virtana. My week has been spent learning the pybullet Python library using Python 2.7 and matrix mathematics. Thus far my days have consisted of running the pybullet examples and try to understand them to be able to make simple simulations using the included models, learning how the camera is works, understanding view and projection matrices, and controlling robots in a simulation.
To learn the pybullet library, I have been reading their quickstart guide. I stared by trying to understand how to put the models in the world and their positioning. At first, I wasn’t sure how to move the view in the world and that made looking at what I was doing harder than it should have been, but I did eventually learn it.
Then I had to learn how to take pictures of the world using their camera API and display it in Matplotlib. I had to reshape the output from the camera using Numpy to actually be able to display it.
Once I had an idea of how the camera was working, I moved on to the robots. I had to learn about the base, links, joints and how to move them. There are some topics that I were introduced to that I have like inverse kinematics which I have no clue as how it works. All I know is that the pybullet API gives me the answer.
I had to learn how make a view matrix using the homogeneous transformation. The work included getting the position (a point vector) and orientation (a quaternion) of the robot, and manipulating them into a view matrix.
Mathematics Reference
Note: My explanations of the mathematical concepts are coming from someone who is learning it on the job, and doesn’t have a Mathematics nor Engineering degree. I only understand some of it thanks to my boss explaining it to me to try to get a picture.
Rotation Matrix
Example rotation matrices
Rotation in the x-axis
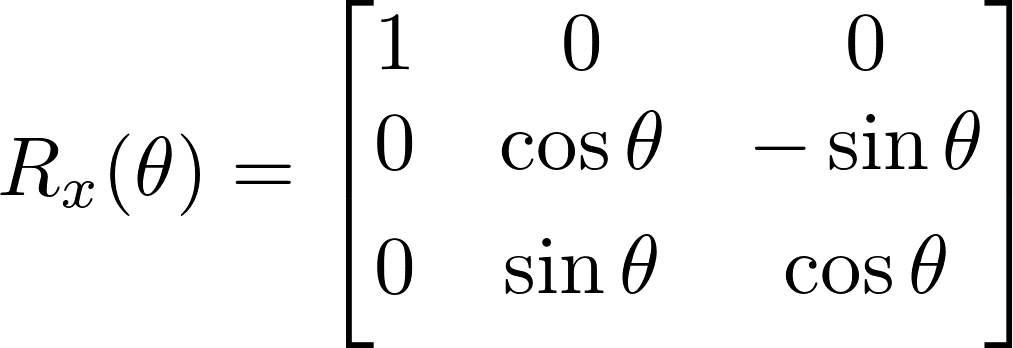
Rotation in the y-axis
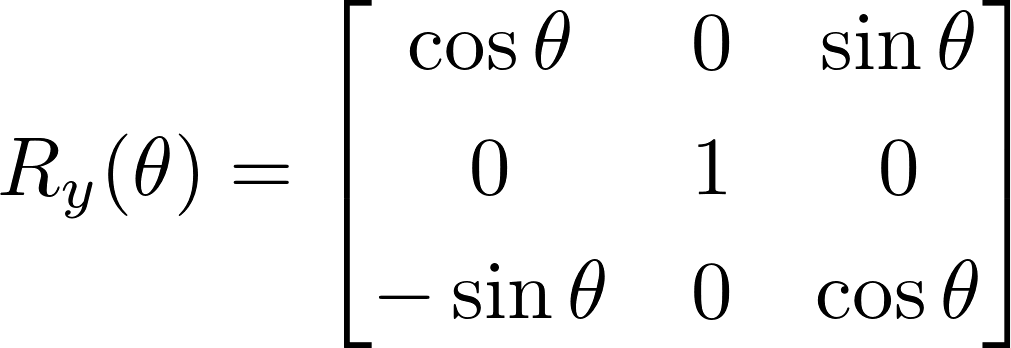
Rotation in the z-axis
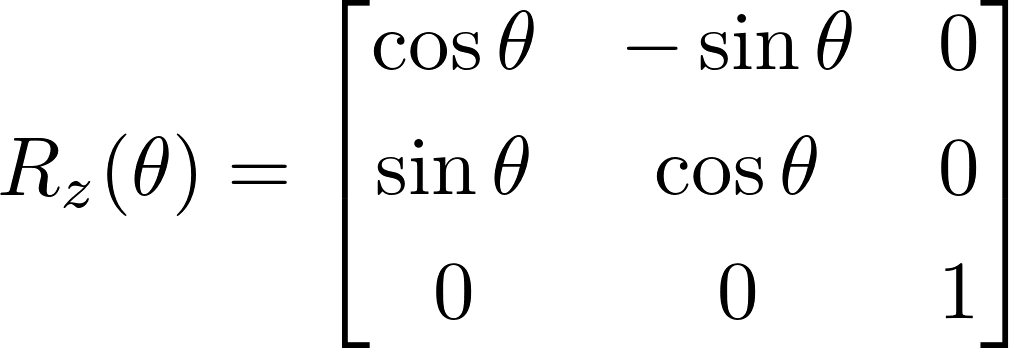
Homogeneous Transformation
In simple terms, it is matrix that maps coordinates with respect one reference point eg. point about the robot to coordinates with respect to another reference point eg. the origin of the world.
Below is a diagram explaining how to make the matrix is made.
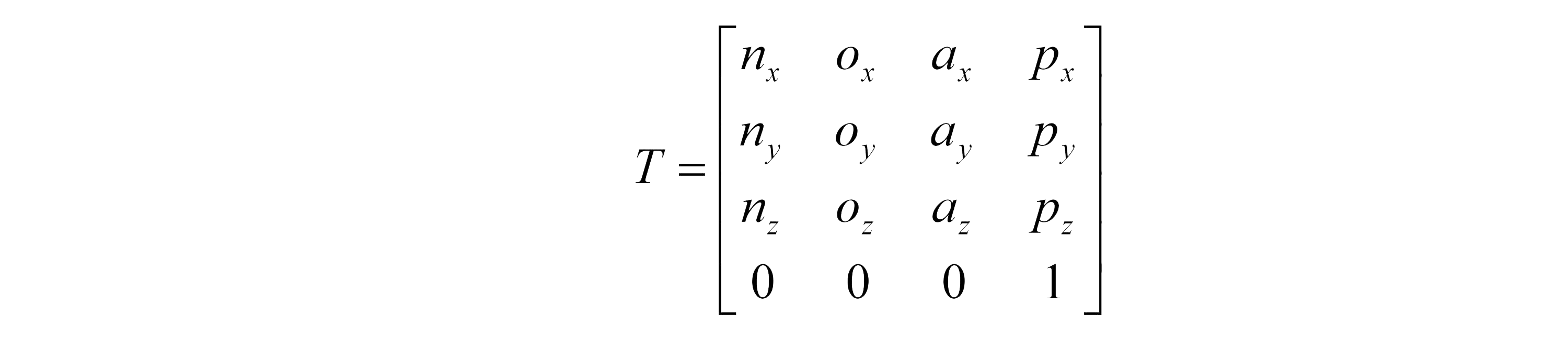It contains a 3*3 rotation matrix, a 3*1 point vector and the last row is [0 0 0 1].
Quaternion
It is basically a set of values that define an object’s orientation.
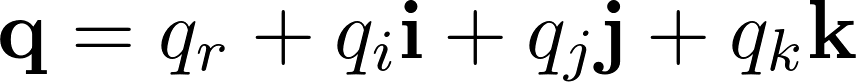
The following shows how it can be used to generate an equivalent rotation matrix
